Зміст
Думаю, ви напевно помічали, що деякі явища пов’язані між собою. Наприклад, температура повітря на вулиці і кількість людей, що прогулюються, час доби і кількість друзів онлайн в соцмережі, добробут країни і кількість нобелівських лауреатів (хоча тут все ж таки спірно). Одні явища пов’язані сильніше, інші слабші, і сила зв’язку називається кореляцією . Її вимір має безпосереднє відношення до портфельного інвестування та диверсифікації інвестиційних активів .
А завдяки розрахунку коефіцієнта кореляції ми можемо дізнатися про силу взаємозв’язку в конкретному числовому вираженні. Це дуже зручно і корисно при аналізі даних у різних галузях науки, у тому числі в економіці та інвестуванні.
Сьогодні я розповім вам докладніше про те, що таке кореляція простими словами, без складних формул та термінів. Також я покажу вам, як правильно та легко розрахувати коефіцієнт кореляції в Excel та як правильно інтерпретувати результати, щоб використовувати їх для складання інвестиційного портфеля.
Що таке кореляція простими словами
Не хочу вас відразу вантажити формулами та розрахунками, про це поговоримо ближче до кінця. Давайте спочатку розберемося, що за своєю суттю означає цифру коефіцієнта кореляції, яку ви можете зустріти в якійсь книзі чи статті.
Значення коефіцієнта може змінюватися від -1 до +1:
Якщо значення близьке до одиниці або мінус одиниці — це означає, що два явища так чи інакше сильно взаємопов’язані. Втім, причини цього не завжди очевидні — явище А може впливати на явище B, навпаки. Нерідко буває, що існує явище C, яке надає руху А і В одночасно. Загалом природа кореляції — це вже друге питання, яким мають займатися дослідники.
Навколонульові значення, у свою чергу, говорять про відсутність будь-якої залежності між явищами. Немає конкретної межі, де закінчується випадковість і починається взаємозв’язок, все залежить від предмета дослідження та кількості даних. Навскидку, зазвичай при значеннях від -0.3 до 0.3 можна говорити, що залежність відсутня.
При високій позитивній кореляції за графіком А росте і графік B, і що вище значення, тим злагодніше обидва рухаються. Для наочності, ось як виглядає кореляція +1:

Рухи графіків повністю повторюють один одного, причому це як у разі простого додавання, так і з множником.
За сильної негативної кореляції зростання графіка А призводить до падіння графіка B і навпаки. Ось так виглядає кореляція -1:

Рухи графіків нагадують дзеркальні відображення.
Коефіцієнт кореляції – зручний інструмент для аналізу у багатьох сферах науки та життя. Його легко розрахувати в Excel і застосувати, тому найбільша складність у роботі з ним грамотно підібрати дані для розрахунку. Основне правило — що більше даних, то краще. Багато взаємозв’язків виявляють себе лише на довгій дистанції.
Також потрібно стежити за тим, щоб знайдені кореляції були помилковими.
Хибні кореляції
Справа в тому, що за допомогою коефіцієнта кореляції можна перевірити на взаємозв’язок будь-які явища, які можна виразити у числовому вираженні. Тобто реально будь-які — наприклад кількість весіль у Нью-Йорку та обсяг імпорту нафти в США з Норвегії:

Кореляція становила 86%! Чи справді весілля впливають на експорт нафти? Зрозуміло, ні — така залежність є цілком випадковою. Саме так виглядає пастка хибної кореляції – вона може показати взаємозв’язок там, де її насправді немає.
Кореляція та диверсифікація
Як знання про кореляцію активів можуть допомогти краще вкладати гроші? Думаю, ви всі добре знайомі із золотим правилом інвестора – не клади всі яйця в один кошик . Йдеться, природно, про диверсифікацію, яка нерозривно пов’язана з поняттям кореляції. Це вловлюється навіть із назви — англійське diversify означає «різноманітнити», бо як коефіцієнт кореляції якраз показує схожість чи відмінність двох явищ.
Іншими словами, інвестувати у фінансові інструменти з високою кореляцією не дуже добре. Чому? Все просто – схожі активи погано диверсифікуються. Ось приклад портфеля двох активів із кореляцією +1:

Як бачите, графік портфеля у всіх деталях повторює графіки кожного з активів – зростання та падіння обох активів синхронні. Диверсифікація в теорії повинна знижувати інвестиційні ризики за рахунок того, що збитки одного активу перекриваються за рахунок прибутку іншого, але цього не відбувається зовсім.
Портфель дає невеликий виграш у зниженні ризиків – але тільки в порівнянні з більш прибутковим Активом 1. А так, жодних переваг по суті немає, нам краще просто вкласти всі гроші в Актив 1 і не паритися.
А ось приклад портфеля двох активів із кореляцією близькою до 0:

Десь графіки йдуть одна за одною, десь у протилежних напрямках, якогось однозначного зв’язку не спостерігається.
Ми бачимо помітне зниження СКО, а значить портфель буде менш волатильним і стабільніше зростатиме. Також бачимо невелике зниження максимальної просідання , особливо якщо порівнювати з Активом 1. Інвестиційні інструменти без кореляції досить часто зустрічаються і з них має сенс складати портфель.
Втім, це не межа. Найефективніший інвестиційний портфель можна отримати, використовуючи активи з кореляцією -1:

Вже знайоме вам “дзеркало” дозволяє довести показники ризику портфеля до мінімальних:

Незважаючи на те, що кожен з активів має певний ризик, портфель вийшов фактично безризиковим. Якась магія, чи не так? Дуже шкода, але на практиці такого не буває, інакше інвестування було б надто легким заняттям.
Коефіцієнт кореляції та ПАММ-рахунку
З розрахунком кореляції як студент економічного ВНЗ познайомився ще на другому курсі. Тим не менш, довгий час недооцінював важливість розрахунку кореляції саме для підбору ПАММ-портфеля. 2018 дуже чітко показав, що ПАММ-рахунки зі схожими стратегіями у разі кризи можуть поводитися дуже схоже.
Сталося так, що з середини року відмовила не просто одна стратегія керуючого, а більшість торгових систем, пов’язаних з активними рухами валютної пари EUR/USD:

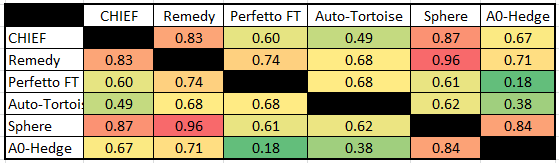
Ринок був для кожного керуючого по-своєму несприятливим, але їх присутність у портфелі призвела до великої просідання. Збіг? Не зовсім, адже це були ПАММ-рахунки зі схожими елементами у торгових стратегіях. Без досвіду торгівлі на ринку Форекс може бути складно зрозуміти, як це працює, але по кореляційній таблиці ступінь взаємозв’язку видно і так:

Ми раніше розглядали кореляцію аж до +1, але, як бачите на практиці, навіть збіг у районі 20-30% вже говорить про деяку схожість ПАММ-рахунків і, як наслідок, результатів торгівлі.
Щоб знизити шанси на повторення ситуації, як у 2018 році, я вважаю, що в портфель варто підбирати ПАММ-рахунки з низькою взаємною кореляцією. По суті, нам потрібні унікальні стратегії з різними підходами та різними валютними парами для торгівлі. На практиці, звичайно, складніше підібрати прибуткові рахунки з унікальними стратегіями, але якщо добре покопатися в рейтингу ПАММ-рахунків, то все можливе. До того ж, низька взаємна кореляція знижує вимоги для диверсифікації, 5-6 рахунків цілком вистачить.
Кілька слів про розрахунок коефіцієнта кореляції для ПАММ-рахунків. Дістати самі дані відносно нескладно, в Альпарі прямо з сайту, для решти майданчиків через сайт investflow.ru. Однак із ними потрібно зробити невеликі перетворення.
Дані про прибутковість ПАММ спочатку зберігаються у форматі накопиченої прибутковості, нам це не підходить. Кореляція стандартних графіків доходності двох прибуткових ПАММ-рахунків завжди буде дуже високою, просто тому, що всі вони рухаються у правий верхній кут:
У всіх рахунків позитивна кореляція від 0.5 і вище за рідкісним винятком, то ми нічого не зрозуміємо. Реальну схожість стратегій ПАММ-рахунків можна побачити лише за денними доходами. Розрахувати їх не дуже складно, якщо знаєте потрібні формули доходності . Якщо прибуток або збиток двох ПАММ-рахунків збігаються по днях і відсотках, висока ймовірність, що їхні стратегії мають спільні елементи — і коефіцієнт кореляції нам це покаже:

Як бачите, деякі кореляції стали нульовими, деякі залишилися на високому рівні. Ми тепер бачимо, які ПАММ-рахунки справді схожі між собою, а які не мають нічого спільного.
Насамкінець давайте розберемося, що робити і як порахувати кореляцію, якщо у вас виникла потреба.
Коефіцієнт кореляції в Excel та формула розрахунку
Мабуть, вас цікавить, як самостійно розрахувати кореляцію двох інвестиційних активів. До винаходу комп’ютерів доводилося робити це вручну, для чого використовувалася така формула коефіцієнта кореляції:
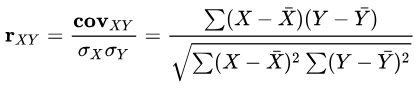
- Rxy – коефіцієнт кореляції;
- COVxy – підступ змінних X і Y;
- σX, σY — стандартне відхилення змінних X та Y
- X та Y з рисою — середнє значення Х та Y
До речі, студентам на іспиті досі комп’ютерів не видають, хоч калькулятор можна й на тому спасибі. Як ви розумієте, заняття все одно трудомістке 🙂
Професійному інвестору може знадобитися розрахувати сотні кореляцій, тому варіант за формулою не підходить. Звичайно, це завдання вже давно автоматизована, і, як на мене, найпростіше розрахувати коефіцієнт кореляції в Excel.


